Pi day is over, but it seems fitting to continue exploring. Archimedes did more than develop an approximation procedure for pi! There are many excellent websites that explain the following in greater detail and discuss many more of Archimedes' theorems about parabolas and tangents. I attempted to draw a diagram using Draw in Word. It's crude but you'll get the idea. The object is to share this extraordinary piece of history of mathematics and have your students finish the proof that a light ray from the focus that strikes a parabolic surface is reflected in a ray that is parallel to the axis of the parabola. This is equally interesting in reverse: External light rays and other forms of electromagnetic radiation that are parallel to a parabola's axis are reflected to the focus, very useful for radar and other 'collection' devices.
Considering that Archimedes' proofs used only geometric properties makes his work even more astounding (now of course we can use coordinate geometry, calculus, etc.). This type of investigation is usually deferred to College Geometry courses, but I believe we can deliver it to motivated geometry, 2nd year algebra or precalculus students. If nothing else, it makes for a wonderful long-term project!
Ok, here goes...
In the diagram below, I've gone out of my way to make the reflecting ray NOT look parallel to the axis, even though we're trying to prove it is. This is to help students avoid assuming collinearity, when, in fact, that needs to be proved!
The two angles marked X are equal by a reflection principle (angle of incidence equals...). The two angles marked Y are equal because it can be proved that the tangent line at P is the perpendicular bisector of segment FP', where F is the focus and P' is the foot of the perpendicular from P to the directrix. I chose not to derive Archimedes' very subtle argument, but it is worth studying the proof. The proof starts by constructing the perpendicular bisector and showing that this line passes through P but no other point of the parabola, thus it is tangent. Alex Bogomolny's excellent and in-depth treatment (with java applets) of this topic (on cut-the-knot) is very worthwhile reading.
The student is being asked to prove that the reflecting ray is parallel to the axis. This is equivalent to showing that the line containing PP' and the reflecting ray are one and the same. The argument is straightforward, but students may want to continue learning more about the genius of Archimedes.
[Good luck copying this diagram (jpg). Some of you may find errors in my argument or an extremely simply argument for the parallelism, so pls share!!]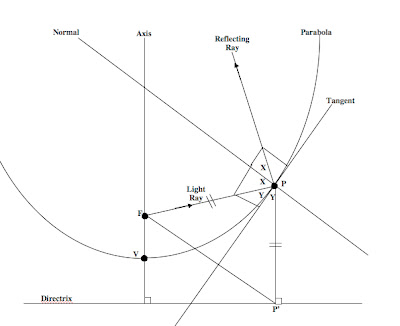
Saturday, March 17, 2007
The Genius of Archimedes: Parabolas, Tangents...
Subscribe to:
Post Comments (Atom)







No comments:
Post a Comment