Products of Digits: Challenges for Everyone...

[You may also want to look at the preview of the interview with Alec Klein, author of A Class Apart, to be hosted on MathNotations. Alec has agreed to answer my questions about Stuyvesant HS in NYC, other specialized schools and gifted education.]


One never knows where the inspiration for a math challenge might come from. This one came from a book I devoured recently, entitled The Righteous Men by Sam Bourne. If you enjoyed the Da Vinci Code and solving the number puzzles and other codes embedded in the story, you will definitely enjoy this novel. One of the most important clues to unraveling the mystery in the story was stated as a riddle:
Just men we are, our number few
Describable in digits two
We're halved if these do multiply
If we few perish then all must die.

Ok, now some of you are going to ignore the math problem and run out to find this book, but for those who would like a more prosaic version of the math problem, here is our first conundrum:
Note: Students from middle school on can attempt some of these although the proofs are a reach.

(1) Determine a 2-digit positive integer the product of whose digits is one-half the integer.
Now, it won't take you long to find such a number (once you get past the elliptical phrasing), but that's just to whet your appetite. The real challenge begins:

(2) Prove that your answer to (1) is unique, i.e., there is only one solution to the problem.

Comment: We're looking for more than an exhaustive search through all ninety 2-digit numbers or a programmed solution. The key to this and all of the remaining questions is to find an approach to solving a single equation which has 2 or more variables whose domain is the set of positive integers. Students are usually not introduced to solving such equations but they appear frequently on SATs and Math Contests. Because we are looking only for positive integer solutions, a standard algebraic approach must be supplemented with arithmetic concepts and testing of several possibilities. Number theorists refer to these as Diophantine equations.

(3) How about 3-digit integers? If 12 were permitted as the hundreds' digit, then (12)96 would satisfy the problem since (12)(9)(6) = 648, which is one-half of 1296. Unfortunately we can't allow that, so your challenge is to prove that there are NO 3-digit numbers (meaning positive integers) the product of whose digits is one-half the number.

Comments: Again, you're confronted with an equation but this time there are 3 variables. One approach is to solve for h in terms of t and u (I'll let you guess the symbolism) but there surely must be numerous possibilities! Or are there...

(4) Since we couldn't find a 3-digit number with the property, we'll rework the ratio:
Determine a 3-digit number the product of whose digits is one-fourth the number.

(5) Of course, I can't let you off the hook that easily. Prove that your solution in (4) is unique!

Standard disclaimer: These results have not been independently verified. Translation: I devised problems (2)-(5) and therefore there could be errors. If you find other solutions, let me know!

Reminder: Don't forget to give Proper Attribution when using these original problems. See the instructions in the sidebar. I appreciate your understanding and acknowledgment.

Taking the 'Unsummable' Numbers to a higher level: An Algebraic Proof

[You may also want to look at the preview of the interview with Alec Klein, author of A Class Apart, to be hosted on MathNotations. Alec has agreed to answer my questions about Stuyvesant HS in NYC, other specialized schools and gifted education.]


Please comply with the 'Proper Attribution' statement that now appears in the sidebar.

Anyone recall a detailed investigation I posted in Feb '07 about numbers which can or cannot be written as a sum of 2 or more consecutive positive integers? You will probably want to quickly review that for this discussion. That investigation was implemented in a 9th grade prealgebra class with students who had struggled with math for a long time. They worked for the entire period (and into the next class as well) and expressed satisfaction and a sense of accomplishment. One student, KC, even found a way to express those numbers which were unsummable!

Today, we will take this question of which numbers are unsummable to a higher level. The challenge for my readers and for students is to use methods from Algebra 2 and basic number theory (primes, factors) to prove a conjecture made by one of my former students.

Quick background:
Students were asked to investigate those positive integers which can be written as a sum of 2 or more consecutive positive integers. I started them off with examples like
3 = 1+2; 5 = 2+3; 6 = 1+2+3, etc.
They worked in pairs and completed a table up to 36 over a couple of days. Most quickly realized that every odd positive integer starting with 3 could be represented but not every even positive integer. Working in pairs helped students to catch common arithmetic/logic errors and the results were reviewed after every 10 numbers or so in order to insure that all students had accurate results to work with.

Here's your challenge for today:
Rather than demonstrate which numbers can be represented as such a sum, your mission is to prove the following:
Powers of 2 are unsummable, i.e., a power of 2 can never be represented as a sum of 2 or more consecutive positive integers.
Notes:
(1) The whole notion of algebraic proof may be new for some students, so this may require some demonstration first.
(2) Students will need to know the formula for the sum of an arithmetic series, so this challenge would be appropriate after learning or reviewing that. The instructor however could develop that formula earlier on or simply provide the formula.
(3) Some understanding of the Fundamental Theorem of Arithmetic is needed here, i.e., every positive integer is either prime or can be written as a product of primes in a unique fashion. This theorem often goes unmentioned or taken for granted in middle school - time to bring it back?
(4) Some readers may find a way to prove this without using the algebraic formula mentioned above. Share that as well!

Enjoy...

Putting the Gold 'Bach' into Primes! An Investigation...

[Now that the 'Carnival is Over' (is that another song title?), it's time to return to the essence of this blog.]

There is no end to the number of articles one can find on the internet and in the literature regarding prime numbers, from famous theorems to unsolved problems that seduce budding young mathematicians.

The following investigation is intended for middle school students, working in research teams, but can be extended to secondary students who want to explore mathematics further in their classroom or in their Math Club.

Student Investigation

Notice that
4 = 2+2
6 = 3+3
8= 3+5
10 = 3+7 = 5+5

The purpose of this investigation is to explore part of the world of prime numbers and become a mathematical researcher. Mathematicians, like scientists, observe phenomena, look for patterns, make conjectures and generalizations and try to prove them. Mathematicians seek to understand the secrets (general truths) underlying patterns and relationships in numbers and shapes.

1. Based on the first few examples above, do you think your mathematical research team has enough information to make a conjecture, or educated guess, about even positive integers? By the way, why didn't we begin the pattern from the first even positive integer, 2?

2. Let's continue the exploration. Begin by making a list of all primes up to 100. Why does it make sense to have this list available?

3. A table is very useful to organize your data and form hypotheses. A suggested table is provided below. One of the column headings needs to be completed. Then complete the table for even integers up to 30. Your team leader should assign a few of these to each member of the team.

Even Positive Integer........Number of Ways to ___............List of ways
4..................................................1........................................2+2
6
8
10...............................................2........................................3+7;5+5
12...............................................1.........................................5+7
.
.
.
30

4. Here's an example of a conjecture:
Based on
22 = 3+19; 5+17; 11+11
24 = 5+19; 7+17; 11+13
26 = 3+23; 7+19; 13+13
28 = 5+23; 11+17
one might conjecture that even numbers can be written as a sum of two primes in at most three ways.
Do you think it's easier to prove this 'educated guess' or disprove it? Try it! You may need to extend your table!

5. Extend your table to even positive integers up to and including 60.

6. Based on this table, your research team now has to make at least three conjectures, then attempt to disprove them or provide an explanation for why they may be true. You may need to go beyond your table.

7. Jeremy determined that
60 = 7+53; 13+47; 17+43; 19+41; 23+37; 29+31 and
100 = 3+97; 11+89; 17+83; 29+71; 41+59; 47+53
He conjectured that six is the greatest possible number of ways that an even number up to 100 can be written as a sum of two primes. Disprove it! Again, you might need to extend your table.

8. Is your research complete? Do you think a mathematician would make other conjectures about even numbers or think of other problems related to sums of primes? Perhaps, numbers that can be written as a sum of three primes? Sums of consecutive primes like 3+5+7. Perhaps you'd like to continue....

9. [When the activity is complete] Research Goldbach's Conjecture on the web and write a brief description of its history. Has it been proved?

As usual, make suggestions for improving this; revise, edit, enjoy...
If you use this in the classroom, please share the experience. The feedback is invaluable to me.

Seventeenth Edition of the Carnival of Mathematics: "At Seventeen, I Learned the Truth"

[This edition of the Carnival is dedicated to our 12-year old Golden retriever, Teddy, who passed away on 9-15-07. He was everyone's 'best friend' and gave far more than he received. When my mom passed away recently, my 4-year old grandson was told that she became a star in the sky. When Teddy died, he comforted us by saying, "Now, Teddy's a star too and Nana will be able to walk him."]


What was the age of the Dancing Queen in an ABBA classic? (ABBA is one of my favorite palindromic groups).
Does anyone remember the title of Janis Ian's classic 60's song about teenage angst and includes the phrase that is part of the title of this post?

As it is becoming a tradition to begin our Carnival with comments on the cardinal number of our edition, I will choose a few more serious facts about 17, one of which I alluded to in the post inviting submissions to this carnival (anyone recall the pdf reference?). The sources here include the Wikipedia article on this number.

From MathWorld, 1/17 = 0.0588235294117647... (repeating). Note that the length of this repeating decimal is 17-1 = 16, which is maximal. I've always been fascinated by such full repetend primes...
17 is the third Fermat prime, as it is of the form 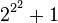. Since 17 is a Fermat prime, heptadecagons can be drawn with compass and ruler. This was proved by Carl Friedrich Gauss. Now you know my pdf allusion: Pierre de Fermat...

17 is known as the Feller number, after the famous mathematician William Feller who taught at Princeton University for many years. Feller would say, when discussing an unsolved mathematical problem, that if it could be proved for the case n = 17 then it could be proved for all positive integers n. He would also say in lectures, "Let's try this for an arbitrary value of n, say n=17." In the class I teach on Wednesday nights, I naturally asked a young lady to give me her favorite number. I kid you not!

I could go on , but this takes away from the excellent submissions, so without further ado, I present to you exactly SEVENTEEN wonderful posts, nominations and favorites of my own choosing. By the way, there is no specific structure or bifurcation. Join me now as we take a pseudorandom walk through a slice of the math blogosphere...

(1,2) Denise over at letsplaymath, sends us two interesting posts:
Egyptian geometry and other challenges and Alex’s puzzling papyrus.
Denise described these fascinating articles:
"...two posts about ancient Egyptian math. The target audience for these was middle school to high school teachers and their students, especially homeschool families (who often try to coordinate their topics of study across the curriculum). The mathematical level is high school geometry or lower."
(3) Denise also included Math Quotes VII (too bad it wasn't XVII!).

(4) Vlorbik recommends that we visit Isabel from God Plays Dice who brings us Why g ~ π².
Don't miss the astute comments, particularly, John Armstrong's concise summary of Isabel's fascinating post:
"What Isabel is pointing out is that at least one definition of "meter" over the years has been designed so that the numerical value of g coincides with the number pi^2."

(5) Vlorbik also links us to a relatively new blog from a brilliant and modest mathematician, William Gowers, who is contributing his insights to mathematics pedagogy. His post, "How should vector spaces be introduced?" reveals his wisdom and humility. Read the comments! Thanks, Vlorbik, for these excellent nominations!

(6) David Eppstein from LiVEJOURNAL brings us into the realm of combinatorics with Not the multinomial coefficients, a 3-dimensional view of binomial coefficients that is not simply an extension of Pascal's triangle. Some combinatorial background is needed here to fully appreciate this but the presentation is clear and engaging.

(7) John Armstrong of the Unapologetic Mathematician brings us a fascinating post on Newton Fractals, a description of Newton's Method and its behavior for f(x)=x³-1, requiring only differential calculus as a background. John develops the root search in the complex plane. By iteration and suitable coloring, John is able to suggest how a fractal is formed. His ability to clearly explain this tells me how very fortunate his students are.

(8) Mathematics in a Jack Reacher Novel is a post in Jeffrey Shallit's blog, Recursivity. Jeffrey discusses extensions of the mathematics suggested in a novel by Lee Child. The main character, Jack Reacher, displays some math-savant characteristics but Jeffrey enriches this with some fascinating problems involving numbers and their digits. Try the exercises and see if you match the results discussed in the comments!

(9) Jonathan from jd2718 offers us Puzzler puzzled. This is Jonathan's specialty, devising variations on famous number puzzles that require considerable thinking outside the box. In this case, one of his students had difficulty with interpreting the language of the original question and suggested another take on the problem. Now we have two great problems to work on!

(10) Mark Dominus from the Universe of Discourse offers The Missing Deltahedron , an advanced geometry article describing some research Mark is doing. Marc is following up his analysis of the convex deltahedra, which are the eight polyhedra whose faces are all congruent equilateral triangles. The problem is that there is a break in the pattern in the number of faces and it seems to upset the harmony in the universe!

(11) Meeyauw shows us an application of geometry to knitting. She mathematically builds on another blogger's post on knitting some of Escher's classics and even found a link to 'crocheting the hyperbolic plane'!

(12) Maria at Homeschool Math Blog brings us Number Rainbows, useful for primary math teachers. The idea is that you connect two numbers with an arc if they add up to a particular number, such as 13. Using different colors to connect these pairs makes an attractive rainbow pattern and may help students learn their addition and subtraction facts. Mathmom, in her comment, suggests an extension to Gauss' method of addition.

(13) Speaking of Mathmom, enjoy her insightful and provocative Calculator Rant. Perhaps the AP Calculus Committee set the gold standard a few years ago by developing a 2-part test, one with and one without the graphing calculator. This approach is definitely filtering down through the grades and Mathmom informs us that this has been adopted for some time by MathCounts.

(14) Andreas, from Figuring Out Computer Science, brings us a discussion of the The Most Important Problems in Computer Science. He sent out queries to some experts in the field and the main theme is that of complexity vs. simplicity, including the P=NP problem. Great quotes here but my favorite is "...simplicity is the ultimate sophistication." (da Vinci)

(15) Jacob from Winter's Haven, was one of the first to submit an article for this carnival:
Pure Math, Applied Math and A Priori Proofs. He presents a thoughtful and logical case for why scientists cannot prove natural phenomenon using only a priori, i.e., theoretical, mathematical arguments, in the absence of empirical corroboration. He explains that mathematics only provides possible models of reality which then need experimental verification. Nice...

(16) Marc has published his original research: New Prime Formula Helps Investigate Prime Numbers. After reading my post on Fallout From the Sieve of Eratosthenes, he thought I might be interested in his discovery and he is helping me to work through the details. Since the unsolved problems related to primes have been a motivating force for so many mathematicians, I know you will enjoy reading this significant find.
And speaking of primes... Coincidentally with my discovering Marc's research, I also found the accounts of the new algorithm developed by 3 mathematicians from India, which is considered a significant breakthrough in primality testing. You can find the fascinating details here and here.

(17) And last but certainly not least, Kurt over at Learning Computation threw Greg Muller's 'hat into the ring' by nominating Greg's engaging Hat Guessing Puzzles, The Revenge. Greg's blog is The Everything Seminar and if this is a sample of his writing, I plan on returning. The hat-color-guessing puzzle is itself is a fun exercise in logic for all of us, but Greg shows us how it is related to error-correcting codes in computer science.

Well, there it is. Exactly XVII excellent offerings. Enjoy them!

By way of disclaimers, I sincerely apologize for any omissions, invalid links, or errors of commission I may have made. Just let me know and I'll correct them. If you sent in your submission after 12 AM on Fri 9-21-07, it might not have made it into this Carnival, but I will post an addendum and errata if needed.

BTW, if you're wondering why I've made no mention of the Prof. Steen interview and the ongoing commentary, well, I think I just did...

Addenda/Errata:
Correction has been made in the link to #10: The Missing Deltahedron. Other links should be working as well. Sorry for any inconvenience caused by this.

A Special Case of the Random Triangle Problem

jd2718's fascinating discussion regarding selection of a random triangle a couple of weeks ago led me to consider the strategy of particularization, aka, 'consider a special case' or 'make it simpler', approaches I typically suggested to students when faced with a problem that was confusing, vague or overly general. Instead of phrasing it in terms of geometric probability, I've reduced it to a much simpler problem, followed by a locus problem, a topic perhaps currently underemphasized.

First a 'simpler problem' fro your geometry students:

Consider points A(-3,0) and B(3,0) in the coordinate plane. If C(x,y) is a point in the plane such that angle ACB is a right angle, determine the value of x² + y².
Note: Many capable students would rush into the distance formula and the Pythagorean Theorem, but there is another approach that is less algebraically cumbersome!

Now for more generalization...

The following questions regard points in a single plane. If A and B are 2 arbitrary points in a plane, d units apart, determine the locus of all points C in that plane such that
(a) Angle ACB is right
(b) Angle ACB is acute
(c) Angle ACB is obtuse

Notes:
(i) Why do you think I chose to focus on angle ACB rather than triangle ACB as in Jonathan's discussion?
(ii) If students are unfamiliar with the term locus, rephrase as "Describe the set of all points C such that..."
(iii) Will this question lead directly to solving the general probability question raised by zac or Jonathan? Probably not, but I was thinking more in terms of accessibility for most geometry students. The open-endedness of the original triangle problem is highly instructive and can lead to profound considerations but that can be tackled later...

Interview with Prof. Lynn Arthur Steen - Part II

This is the second and final part of my online interview with Prof. Steen. Part I is posted here. It includes useful background information about the new Algebra II End-of-Course Exam, its purposes, its content and its impact on districts that use a 3-year integrated math sequence. Prof. Steen also courageously tackles issues as diverse as proficiency with fractions, the role of factoring in the 21st century, AP Calculus as a model for a national curriculum, the linear mastery model of learning mathematics, gifted education, the critical factors needed to elevate mathematics education in our country, and attempting to resolve the Math Wars. He ends with advice for mathematics educators, restating the core message of the NCTM Standards.

Again I want to express my gratitude to Prof. Steen for taking the time to reply thoughtfully to some difficult and controversial questions regarding mathematics education. I'm hoping that this forum serves as a springboard for other bloggers to have further conversations with educational leaders and, perhaps, bring, opposing parties together at an 'online roundtable.' Regardless of personal ideologies, I hope those who have or will visit will find this interview as thought-provoking as I did. One thing is for certain. Both Prof. Steen and I have a new-found appreciation for how difficult it will be to resolve the major problems in education, mathematics education in particular. Again, I invite readers to post comments and keep the discussion alive. I would also be interested in reactions to the format of this interview. Suggestions for improvement? Perhaps make it more give-and-take?

Math Notations Interview (continued)

Lynn Arthur Steen, St. Olaf College, September, 2007

6. Many secondary teachers decry the lack of proficiency with fraction skills and fraction concepts demonstrated by their students. It’s always easy for each group of teachers from graduate school on down to place blame on prior grades. Do you believe that Achieve has addressed this problem adequately with their enumeration of K-8 mathematics expectations in their 2002 publication, Foundations for Success?

The expectations summarized in Foundations for Success certainly subsume the arithmetic of fractions and the relationships among fractions, decimals, proportions, and percents, but they do so quite concisely. Details are unfolded in Achieve's K-8 Number Benchmarks, especially throughout grades 4-6. However, no one associated with this project was so naïve as to imagine that the mere inclusion of an extensive discussion of fractions in a report will adequately address the problem of students entering high school—or college, for that matter—without understanding fractions. Setting out clear expectations is only a first step.

7. What is your position on the role of technology, calculators in particular, in K-4, 5-8 and 9-12 mathematics classrooms?

My view is that students should learn to use technology wisely, carefully, and powerfully. By wisely, I mean that they make conscious and appropriate decisions about when to use calculators or computers, and when not to. By carefully, I mean that they think enough about the problem they are working on to recognize when a calculator or computer result is beyond the realm of plausibility. By powerfully, I mean that they make full use of the most powerful tools available in order to prepare rich and accurate analyses. In this age, mathematical competence requires competence to use computer tools, so the use of technology must be an explicit goal of mathematics education.

It no more follows from students' widespread misuse of calculators that calculators should be banned than from students' widespread misunderstanding of fractions that fractions should be avoided. Use of technology is as important as use of fractions, and both need to be taught and tested.

8. I have stated repeatedly on this blog that the Advanced Placement Calculus syllabus from which I taught for over 30 years, is essentially a national curriculum for calculus and that I strongly endorse it as such. Do you agree with this characterization? Do you see projects such as ADP moving in a similar direction, working closely with states to achieve a common set of mathematics topics K-12 that must be covered at each grade level?

As AP courses go, AP calculus is one of the best. By intent of its sponsor (the College Board), it follows rather than leads national trends. For example, the most recent revision took place a few years after (not before) implementation of pilot projects supported by NSF's calculus reform program. The momentum for change was lead by college faculty, not by the College Board. ADP has a more ambitious goal, namely to lead the nation's K-12 schools to higher standards. In contrast to AP calculus whose syllabus is in the mainstream of college calculus courses, the expectations produced by MAP and ADP are on (and sometimes beyond) the leading edge of K-12 mathematics programs.

9. The types of problems Singaporean children, for example, are tackling seem more complex than their grade counterparts in the U.S. Do you believe that most mathematics curricula in the US, particularly in the area of problem-solving, are as challenging as those in other high-performing nations?

U.S. education clearly lags behind many other nations. This is not just a matter of curriculum but of teacher preparation, time in school, parental expectations, community environment, and perhaps funding. Some other nations (e.g., Japan) decided that their curricular expectations were too high and have reduced them. Others (e.g., England) have seen student performance fall. As I implied in my answer to the previous question, the MAP and ADP expectations, being calibrated to international standards, are well beyond what can be achieved at this time by most districts for most students. Their purpose is to set a target, but to reach that target we will need to change much more than curriculum.

10. The End-of-Course Algebra II exam will have a central core and 7 optional modules. Why were traditional topics such as log functions, matrices, conics and sequences/series pulled out of the core? Also, were the standards influenced by the Algebra II topics currently included on the SATs?

The traditional Algebra II course was developed as a stepping stone to calculus for the minority of students who felt they might want to study further mathematics. Two decades ago fewer than half of the age cohort took Algebra II. Today's course is intended for all students; it is a requirement for high school graduation in more than half the states. So it is natural that the "core" of Algebra II be rethought, with more specialized topics set aside into optional units. The new Algebra II may well be the last mathematics course ever taken by many of today's high school students, so I hope that the topics included in the new syllabus and test are well suited to the needs of all students.

I say "hope" because I actually know very little about the details of the test development process. In particular, I do not know if anyone has made any effort to coordinate topics with the revised SAT.

11. I’m assuming that school districts are already or soon will be receiving more detailed information concerning the new End-of-Course Algebra II exam. Will there be a full sample practice test made available? The Achieve web site will be helpful to Algebra II teachers, but could you suggest some additional resources they could use?

I am even more ignorant of these implementation issues than I am about the course goals. While it is helpful to see sample tests, the best way to prepare for an Algebra II test is to study a wide variety interesting and challenging problems. The internet is full of sites that offer enrichment and challenge problems for different high school courses. I'd suggest exploring the Math Forum in the United States and the Millennium Mathematics Project in the United Kingdom.

12. In your opinion, how will the End-of-Course Algebra II exam impact on those districts that use a 3-year integrated math sequence?

This is a very important question, and relates directly to the issue you raised earlier about what constitutes the core of the course. In my view, since passing the new end-of-course Algebra II exam will be a requirement for high school graduation for many students, it should be thought of more as an exam covering the third year of high school mathematics than as an exam covering algebra topics that are needed for calculus. Clearly there is much overlap in these two perspectives, but there are also some differences. I understand that the strategy of a core test with optional modules is intended precisely to reflect these two options. I remain concerned that the older calculus-focused view remains too dominant, at the expense of many newly-important topics that serve to introduce combinatorics, finance, probability, statistics, computer science, etc.

13. I still have a hard time when a student reaches for the graphing calculator to analyze the signs of the quadratic function f(x) = x^2-2x-8. Most textbook publishers have deemphasized factoring, relegating it to the back of the book. Educators have generally followed suit, although not all. How do you view the role of factoring in Algebra II and the secondary curriculum in general?

Factoring is one of the topics on the borderline of the two perspectives on Algebra II—preparation for life vs. preparation for higher mathematics. For life (e.g., citizenship and personal living) factoring is a relatively useless skill. For higher mathematics, the conceptual role of factors is crucial, but all real problems that may require factors are solved using computer tools (e.g., Mathematica). The only place where actual factoring of factorable polynomials is required on a regular basis is in mathematics courses. My advice is to be honest with students about this skill (and others like it). It is important for certain purposes, but not a life skill.

14. A recent article in Time magazine as well as a recently published book by Alec Klein make a strong case for gifted education and developing the talents of our brightest math and science students. Do you believe that our most talented math students are being adequately served? In particular, do you believe they can they flourish and develop equally well in heterogeneous classes as in fast-track accelerated classes?

This too is a very important and difficult question. Research and experience confirm that the presence of bright and intellectually aggressive students in a class helps propel all students to higher levels of achievement, so pulling these students out will in most cases make it less likely that the average students will reach their full potential. On the other hand, bright students whose mind has moved beyond the class syllabus—which is very common in mathematics—will be bored, resentful, and rebellious. Neither option is good; each short-changes far too many students.

Taking a clue from game theory, it seems to me that a mixed strategy is the best compromise: some work together, some work separate. In addition to raising the bar for average students, mixed groups help accelerated students learn to communicate mathematics—a skill that every client of secondary education—employers and professors alike—report is in very short supply. Separate groups help teachers and students focus on problems that are calibrated to match students' current skills.

However, even when students are separated by skill level, acceleration is not the only option. Mathematically able students should be challenged as much as possible by opportunities for horizontal exploration of optional topics that are not part of the mainstream curriculum. For many students, excessive acceleration is a great disservice. Except for the tiny minority (beyond three sigma) who need to take college mathematics while still in high school, most student who finish the school mathematics curriculum early wind up with a gap between high school and college mathematics, with rushed rather than deep mastery of high school topics, and with little or no opportunity to employ the mathematics they learned in parallel natural or social science courses. It is appalling how often students who receive a passing grade on AP calculus discover upon entering college that they need to take remedial algebra since they have forgotten whatever little they learned in their pre-calculus rush. Far better to slow down, spread horizontally, and dig deeper into the hidden corners of the regular curriculum.

15. Many mathematics educators I’ve spoken to and worked with believe that the learning of mathematics is essentially linear, i.e., one cannot be successful at level D unless one can demonstrate proficiency with levels A, B and C. What is your view on this model of learning mathematics? In particular, do you believe that students need to demonstrate proficiency in arithmetic skills and numeration before moving on to algebra?

The linear model of mathematics learning is wrong in almost every respect. Cognitive scientists remind us that the human brain learns by association, not logic. The history of science is full of examples of researchers who came to parts of advanced mathematics via some phenomenon or theory, not by a logical ladder of mathematical steps. Science students frequently encounter and use parts of mathematics in a physics or biology course well before they encounter it systematically in a mathematics course. Fields medalist mathematician William Thurston once described mathematics as like a banyan tree with branches that take root in different places, providing nourishment and growth along multiple pathways (Notices of AMS 37(1990) 844–850).

It is also extraordinarily counterproductive to our national goals. Dozens of reports have raised alarms about shortages of mathematically trained graduates from schools and colleges. Curricula and requirements based on the assumption that there is just one proper path to mathematics artificially and unnecessarily restrict potential mathematics graduates to those who find an intellectual kinship with that preferred approach. It cuts out those who might approach mathematics from other directions, be it from biology, or statistics, or computers, or finance, or construction, or energy, or environment, or any of a dozen other things that may interest students more than mathematics but which share a side door to mathematics.

16. Many states ‘talk the talk’ about higher standards and expectations, but translating these goals into reality in the classroom has proved difficult. Could you rank order the most important factors that are needed to accomplish these goals? For example, would you place teacher preparation above textbook quality?

Enthusiastic and imaginative teachers who are both mathematically and pedagogically competent are more important by far than anything else in the educational system. In particular, competent teachers need to be free to teach in whatever way is effective for them—which implies minimum constraints from state- or district-imposed curricula and tests. Imaginative teachers with minimum constraints would produce a lot of innovation; required standards and high stakes tests tend to stifle innovation. Clearly, some common expectations and assessments are important, but they should focus on the broad goals of education, not on narrow particulars.

Why do we get narrow particulars (that is, "standards") instead of imaginative teachers? The answer is obvious: money and political commitment. It is cheaper by several orders of magnitude to convene a consensus process to write standards than to attract, educate, and retain people with the interests and skills needed to teach mathematics well to all our nation's students. When you don't have enough teachers with the required competence, then the way politicians "make do" is to lay out specific standards and assessments for everyone to follow. I don't think we have much evidence that this strategy will work.

17. Hindsight is always 20-20, but if you could go back in time to the development of the original NCTM standards, what are some changes you would make, in light of what has transpired over the past two decades?

It is important to remember that at the time NCTM published its 1989 Standards, the very concept of standards was a subversive idea. Even the definition was in dispute: some viewed a standard as a banner to march behind, others as a hurdle that must be cleared. In this context, it was proper for NCTM to be somewhat cautious. Certainly there were places in the Standards where intentions were not adequately communicated, but nothing can ever prevent critics from selective reading. It is only human to read into a text what you want to find. Consequently, different readers read the Standards differently.

I read them as clarion call for eliminating the tradition, most evident in mathematics, to select and educate only the most able students and to provide others, disproportionately poor and minority, with only the illusion of education. For the first time a powerful national voice said that all students deserve a mathematics education. How this can be done, and how long it should take, are details that are still being worked out (as your earlier questions about MAP, ADP, and Algebra II attest). This commitment, that every student deserves an equally good education, is the one unequivocally positive aspect of the No Child Left Behind (NCLB) law.

If I were able to go back and make any change, I would highlight that central message more, and make clear that the suggested particulars were to be worked out through traditional American strategies of local innovation. The mistake NCTM made, if it can be called a mistake, was to let its critics define its message as the particulars rather than to keep the nation's attention on the central goal of providing all students with a meaningful mathematics education.

18. Here’s an innocent little question, Prof. Steen! The current conflicts in mathematics education are usually referred to as the Math Wars. In your opinion, what were the major contributing factors in spawning this conflict and how would you resolve it?

There are many factors involved. I think I can identify a few, but I have no confidence that I could resolve any of them.

One is the natural tendency of parents to want their children to go through the same education that they received—even when, as often is the case with mathematics, they admit that it was a painful and unsuccessful ordeal. This makes many parents critical of any change, most especially if it introduces approaches that they do not understand and which therefore leaves them unable to help their children with homework.

Another source were scientists and mathematicians who pretty much breezed through school mathematics and who were increasingly frustrated with graduates (often their own children) who did not seem to know what these scientists knew (or thought they knew) when they had graduated from high school. Our weak performance on international tests appeared to provide objective confirmation of these concerns, and they came to pubic notice just as the NCTM standards became widely known in the early to mid-1990s. Even though very few students had gone through an education influenced by these standards, the confluence of events led many to believe that the standards contributed to the decline.

A third source can be traced to the way in which the NCTM Standards upset the caste system in mathematics education. Mathematicians are accustomed to a hierarchy of status and influence with internationally recognized researchers at the top, ordinary college teachers in the middle, below them high school teachers, and at the very bottom teachers in elementary grades. The gradient is determined by level of mathematics education and research. So it came as somewhat of a shock to research mathematicians when the organization representing elementary and secondary school teachers, seemingly without notice or permission, deigned to issue "standards" for mathematics. Mathematicians would say, and did say, "we define mathematics, not you."

I could go on, but won't. But I do want to add that, as with any contentious issue, face-to-face dialog helps bridge differences. With some exceptions, I believe that has happened with protagonists of the math wars. Achieve was one of the first organizations to bring to one table people from all these different perspectives. Subsequently, other groups have made similar efforts, generally with good results. As mathematicians and educators roll up their sleeves to work together on common projects, each learns from the other and the frictions that led to the math wars begin to reduce.

19. Finally, I’ve observed considerable frustration among K-12 mathematics educators for the past 20 years. Each wants to do what she/he perceives is the best for her/his students but they are often mandated to follow new curricula and programs that come and go every few years and for which they often receive inadequate training. What message would you like to convey to these dedicated professionals?

I said above that teachers are the key to success in mathematics education, but that outsiders impose standards and assessments as a means of protecting students against soft spots in the system. This is not unreasonable, since in the K-12 sector the state is responsible for guaranteeing that children receive a proper education. It seems to me that the only way that teachers can regain control over their own affairs is for them to convincingly take on the role of ensuring quality education for all children. That will require much higher standards for initial licensure, for tenure, for professional development, and a commitment to post-tenure reviews. This is the regimen followed by most good colleges and with suitable modification, by hospitals. Self-imposed quality control is the sign of a true profession.

The problem teachers face is a severe mismatch between the needs of K-12 education, especially in mathematics and science, and available resources. But here teachers have an asset that they need to make better use of, namely, regular access to parents and school boards. What they need to do with that access is help the public understand the changing nature of mathematics and science, the unique value it offers their children, the challenges involved in keeping up with a rapidly changing discipline while at the same time teaching students of quite varied skills and preparation, and the concrete steps that teachers have taken to ensure that all students receive a sound education. Focusing on quality for all—the core message of the NCTM Standards—should gradually elevate the respect in which teachers are held and with it, the support they receive from the public.

Invitation to Carnival of Math Edition 2^(2^2)+1

While we're waiting for Part 2 of Prof. Steen's interview, please don't forget that MathNotations is hosting the seventeenth edition of the Carnival of Mathematics on 9-21!
I've already received 3 submissions and I'm hoping for many more. In addition, I have found at least one website of original math research I will be sharing with you. There may be some other surprises and even an exciting discovery in mathematics to share as well.

I'm considering dedicating this Carnival to a close friend of mine. I'll only give you his initials in lowercase: pdf
[You have only 30 seconds to solve the riddle!]

As I requested in Edition X and Kurt did in Edition XVI, I am asking math bloggers to submit one or two of their recent posts by either:
(1) Emailing me at dmarain at gmail dotcom (preferred!)
(2) Filling out the blog carnival form

If emailing, pls include the exact phrase Carnival of Math in the subject line and include the following:

(a) title of and permalink to your post
(b) name of your blog and link to home page
(c) an overview of the mathematical content, particularly if highly technical or advanced
(d) your general target audience (e.g., "This posting was designed for ...")

Don't forget that you can also recommend a couple of articles from some of your favorite math bloggers whose light might be hidden under a bushel and deserve recognition. I may do the same.

Since a carnival is supposed to be marked by merrymaking, let's have some fun with this! I'm not as creative as some other hosts, but I'll try to make it interesting.

Please try to send your submissions by Wed 9-19 so that I have the time to do justice to them - thanks!

Interview with Prof. Lynn Arthur Steen - Part I

Update on 9-14-07: Part 2 of the interview is now posted!

[The comments and reactions are beginning to pour in here and on others' blogs. SteveH's and mathmom's give-and-take in the Comments section is a must read -- it's a blog of its own! Part 2 of the interview will be coming on Fri and Mon.]

As reported a few days ago, Prof. Steen, one of the most highly respected voices in mathematics education, graciously accepted an invitation for an online interview at MathNotations. He has been a driving force for the reform of school mathematics for many years and was on the development team that produced NCTM's Curriculum and Evaluation Standards for School Mathematics. For the last few years, he has been involved in Achieve's commitment to developing world-class mathematics standards for K-8 and ADP's similar commitment to secondary mathematics. He will have much to say about these standards and the new Algebra II End-of-Course Exam that will be launched in the spring of 2008. He is a man of great integrity and towering commitment to quality education for all of our children .

A few days ago, I emailed Prof. Steen a set of 19 questions that I felt reflected many of the concerns of my readership and, even more, confronted some of the major issues in mathematics education today. He agreed to reply to all of these, asking only that I publish his remarks in full. My role here was purely reportorial. This is not a debate. Once the questions were composed I stepped back and allowed him free rein. Prof. Steen replied thoughtfully and candidly within 48 hours. MathNotations will publish the interview in 2-3 segments to allow readers to absorb his replies and comment. If you've stopped here by the side of the road, tell your friends and colleagues about it. I invite fellow bloggers to spread the word across the blogosphere as well.

Philosophically, Prof. Steen and I have much common ground, although we diverge on some key points. What I truly believe is that honest dialog is the only way we can move forward, end the Math Wars and reach a strong middle-ground position that best serves the interests of our children. Whatever your ideology may be, Prof. Steen's comments are profound and thought-provoking. Enjoy!

I'll begin with my note of appreciation to Prof. Steen:

Thank you Prof. Steen for your prompt yet thoughtful replies. This has
been a new and rewarding experience for me and I know my regular
readers (and perhaps new visitors) will read your comments with great
interest, regardless of where their ideologies lie. You and I share
many common views and yet we can respect our differences. In the end,
we both want what is best for all our children. There are no easy
answers to difficult questions, however I do believe, as you do, that
dialogs like this will ultimately move us in the right direction.
Thank you again for contributing to this process.
Dave Marain
MathNotations 9-11-07

Math Notations Interview

Lynn Arthur Steen, St. Olaf College, September, 2007

1. Prof. Steen, your involvement in so many mathematics and science education projects is mind-boggling. At this time, what are your greatest concerns regarding mathematics education in the U.S.?

That in our stampede for higher standards we are trampling on the enthusiasms, aspirations, and potential contributions of many students for whom mathematics is best approached indirectly. There is plenty of interesting mathematics in areas such as medicine, technology, business, agriculture, government, music, and sports, but students don't get to see these until large percentages have already given up on mathematics. It is true that mathematics unlocks doors to future careers. But we also need to open more doors to the world of mathematics.

2. Over a dozen years ago, Professor Schmidt, Director of the U.S. participation in TIMSS, made his famous comment about our mathematics curriculum being ‘an inch deep and a mile wide’. He also stressed the importance of having a coherent vision of mathematics education. Since then, fifty states have independently developed sets of mathematics standards and assessments. Although similar in some respects, they lack overall coherence and consistency of high expectations of our children. What is currently being done nationally as you see it to remedy this situation?

Notwithstanding our constitutional tradition of federalism that leaves states responsible for education, some now suggest voluntary national standards as a cure for the incoherence and inconsistency that is evident in state standards. Indeed, Senator Dodd (D-CT) and Representative Ehlers (R-MI) have introduced just such a bill in the Congress. I rather doubt that there is sufficient political support for nationalizing education in this way. Nor do I think it would resolve the problem. It would simply shift the locus of inconsistency from written standards and assessments to teachers and students.

More promising are efforts such as the American Diploma Project Network which is an ad hoc coalition of states that decided to work together on a common education agenda. This is not a "national" effort, but it is more in keeping with the traditions of our nation. Public distribution of comparative data is another strategy for reducing unwarranted inconsistency. Recent studies such as Mapping 2005 State Proficiency Standards Onto the NAEP Scales (NCES, June 2007) that compare states to the common scale established by the National Assessment of Educational Progress lead naturally to improvement motivated by competition or, in some cases, by embarrassment.

Strategies that open more doors to mathematics are more likely to emerge in smaller jurisdictions, for the simple reason that innovation begins locally and the doors that need opening tend to have local roots. So I'm not terribly bothered by lack of coherence and consistency. I'd rather focus first on getting more students to learn more mathematics of whatever kind may interest them. What counts is that students gain sufficient experience with substantive mathematics—not just worksheets—to benefit from its power and, if possible, to appreciate its beauty.

3. What were some of the obstacles faced by Achieve’s Mathematics Advisory Panel, both at the K-8 level and for the secondary curriculum? Were many of the current conflicts in mathematics education (aka, the Math Wars) overcome by this Panel? If not, what issues remain?

This is not a simple question! First, Achieve's formal Mathematics Advisory Panel (MAP) was constituted to work only on the K-8 level and produced Foundations for Success, a report with outcome expectations and sample problems for the end of grade 8. When work moved into the secondary level, it became part of the American Diploma Project (ADP) and operated with an evolving set of advisors representing all levels of mathematics and mathematics education.

From the perspective of the "math wars," the original MAP panel was, for its time, a remarkably catholic forum. Strong voices from many different perspectives set forth conflicting views. Compromises were agreed to, and sometimes reversed after further discussion. Eventually a report emerged. No one was pleased with every detail, but I believe it is fair to say that everyone on the MAP committee agreed that as a whole it represented a good step forward.

We reached this point by agreeing to set aside issues of pedagogy and to concentrate only on content. We further agreed that lists of expectations were less capable of conveying our intent than were rich examples. That is why the final report had 8 pages of expectations and 130 pages of examples. It was far easier for the diverse MAP members—protagonists, witnesses, and victims of the math wars—to agree on the quality of a problem than on the wording of a standard.

We also choose to largely ignore the issue of calculators because it was one of the wedge issues on which we all knew that the panel could never agree. Some may view this as cowardice, and it may be that. However, it made possible the rest of the work and affirmed, in a sense, that issues such as this may best be left for local decisions.

Another wedge issue we faced head-on, namely the place of quadratic functions and quadratic equations. Here we compromised, setting an ambitious bar for end of eighth grade at completing the square with a deliberate mandate to not employ the quadratic formula until the next algebra course. The purpose, of course, was understanding rather than calculation, a goal that in this case everyone around the table could support.

Those on the panel with the most school experience worried that completing the square was much too ambitious. They were proved right in subsequent reviews from states who wanted to use the Foundations for Success as a guide for their own standards. Consequently, later Achieve documents dealing with the transition from elementary to secondary mathematics are much more realistic about just how much algebra can be expected for all students prior to ninth grade.

Secondary mathematics is part of Achieve's ADP effort; the benchmarks together with sample postsecondary tasks appear in Ready or Not: Creating a High School Diploma That Counts (Achieve, 2004). There the contentious issue concerned the quantity of mathematics, especially of algebra, that should be required of all students for a high school diploma. A compromise was reached in which certain benchmarks, marked with an asterisk, were described as recommended for all but only required for those "who plan to take calculus in college." Of course, this asterisk mildly undermines the nominal goal of the ADP enterprise, namely, to set a uniform standard for an American high school diploma.

These matters—the role of calculators, the amount of algebra—are but two of the issues that remain fundamentally unresolved both within the ADP networks and among individuals who care about school mathematics. Other sources of continuing disagreement concern the role of data analysis and statistics, the place of financial mathematics, the importance of arithmetic "automaticity" and a host of pedagogical issues that, as I noted, Achieve largely leaves to others.

4. I’ve expressed great concern on this blog about the lack of frontline teacher representation on these major panels, particularly the President’s National Mathematics Panel? I’ve reiterated my call for redressing this situation via numerous emails to the Panel and on this blog. To date, all such requests have been politely dismissed. How do you feel about the need for increased teacher representation on this and other panels? Was there more K-12 representation (current classroom educators) on the Mathematics Advisory Panel on which you served?

The names of all those who advised Achieve on its MAP and ADP projects are listed in the reports of these projects. Different individuals contribute different types of work: some meet in panels; some review drafts; some write standards or contribute problems. My impression is that quite a few of Achieve's mathematics advisors have taught K-12 mathematics, but relatively few were serving as "frontline teachers" at the same time as they were helping with the Achieve work. Frontline teaching doesn't leave that much spare time.

Generally, I find concerns about representation less important than those about relevant experience. Sometimes the complaint is about the lack of teachers, other times about the lack of mathematicians; often complaints are accompanied by qualifiers (e.g., "current classroom teachers," or "active research mathematicians") that appear to imply that those who do not meet the condition are somehow less capable. What matters is that a panel as a whole include individuals with a broad balance of experience, which for mathematics education certainly includes both mathematical practice and classroom teaching—but not necessarily all at the same time the panel is meeting.

5. Many critics of NCTM’s original 1989 Curriculum and Evaluation Standards for School Mathematics and the revision in 2000 have claimed there was not enough emphasis on the learning of basic arithmetic facts. In your opinion, is the issue primarily due to lack of clarity in the standards, or is there a real difference of position between NCTM and its critics on the importance of arithmetic facts?? What is your position on the relative importance of the automaticity of basic facts?

There is a range of opinion about the importance of arithmetic facts within NCTM, within the broader mathematical community, and within the public at large. I understood the 1989 Standards to acknowledge this fact. A chief insight of statistics is recognizing the importance of variation. Student and adult skills with arithmetic vary, so the goals of mathematics education must take this into account. Almost all disputes about NCTM's standards arose because the historic absolutes of mathematics were replaced by alternatives and variations. In this sense, the critics were right: the Standards made mathematics "fuzzy" by insisting that most problems can be solved in more than one way. In fact, they can be.

There is no dispute that knowing arithmetic facts is more desirable than not knowing them, and being quick ("automatic") is better than being slow. The issue is: how important is this difference in relation to other goals of education? It is a bit like spelling: being good at spelling is more desirable than its opposite, but there are plenty of high-performing adults—including college professors, deans, and presidents—who are bad spellers. They learn to cope, as do adults who don't instantly know whether 7 x 8 is larger or smaller than 6 x 9.

For what it's worth, my "position" is that every child should be taught to memorize single digit arithmetic facts because if they do so everything that follows in school will be so much easier. But failure to accomplish this goal should not be interpreted as a sign of mathematical incapacity. Indeed, both students who achieve this goal and those who do not should continue to be stimulated with equal vigor by other mathematical topics (e.g., fractions, decimals, geometry, measurement), just like both good and bad spellers continue to read the same literature and write the same assignments.







Part II is now published. I hope to hear from many of you!
Dave Marain

Another Problem from Singapore Grade 6B Placement Test

Note: As usual, the comments section contains insightful contributions from Denise, mathercize et al. I expounded briefly on a ratio approach and provided a link to some other bar diagram solutions. By the way, I've been using the misnomer, 'fraction bars' instead of the correct phrase bar diagram. I have a lot to learn here...

Lots of traffic from people viewing this placement test. The following is Question #11 from this test and I think it can lead to fruitful discussion of methods and strategies for middle school and secondary students. Older students will usually use an algebraic approach, prealgebra students might use 'Guess-Test-Revise' with a calculator. However, Singapore students apparently use a 'fraction bar' model for many of these, which I see as a ratio approach. How would you solve it? How would you present this to your students? What methods would you expect your students to use? What percent of your students would feel they don't even know where to begin and give up quickly? Would group work help here?

My first inclination was to set up an equation in one variable, however, because it was on the Singapore test, I tried a ratio approach which enabled me to solve it mentally. Have fun! By the way, to personalize it for your students, you may want to change the names to two students in your class and place it in the context of spending money at the mall!

Also, consider that if one were to use 'Guess-Test', it would make sense to start with a number divisible by $48 (since $240 is a multiple of $48, an intuitive student with strong quantitative skills might easily guess the answer!).

The Question:

Peter and Paul each had an equal amount of money. Each day Peter spent $36 and Paul spent $48. When Paul used up all his money, Peter still had $240 left. How much money did each of them have at first?

CoM Edition XVI - Comments & Opinions - Now up at Learning Computation

Kurt kept us in suspense but this latest edition was worth waiting for. Incisive and droll reviews of many excellent math blogs divided into 3 sections; The Good, the Bad and the Ugly. You'll have to read it to determine his classification system. Kurt also referred us to some some excellent posts that he personally found and wanted to share with all of us. Thanks, Kurt, and I hope you're feeling better! The next edition will be right here on 9-21.

Stay Tuned - A Preview of an Interview with Lynn Arthur Steen

Lynn Arthur Steen has graciously agreed to an online interview for MathNotations. He is Professor of Mathematics at St. Olaf College, Northfield, Minnesota and has written numerous books and articles on the teaching and learning of mathematics at the K-14 level. His leadership roles on the national stage, professional interests and activities would require several pages but I will highlight a few of these. For further background refer to his St. Olaf bio.

In 1985, two years after publication of A Nation at Risk, Professor Steen was asked by the National Council of Teachers of Mathematics to join a new Commission to oversee development of "standards" for school mathematics resulting in the publication of their famous 1989 PSSM document. At the same time he joined the Executive Committee of the new Mathematical Sciences Education Board (MSEB) at the National Academy of Sciences. This led, four years later, to his writing the seminal MSEB's "Report to the Nation on Mathematics Education" entitled Everybody Counts. This widely distributed report provided rationale and impetus to the emerging standards movement in mathematics education. This publication has had a profound effect on my career as a mathematics educator.

He is a past president of the Mathematics Association of America (MAA) and has served as chairman of the Conference Board of the Mathematical Sciences. For the past 7 years, he has served as Mathematics consultant and editor to the American Diploma Project (ADP), Achieve, Inc., which has developed the standards for the new Algebra II assessment to be given next spring.

In his 'spare' time, he has focused a lot of energy on quantitative literacy (especially in an interdisciplinary sense), on the increasingly important interface of mathematics with biology, on the integrity and use of educational data (e.g., graduation rates), and, earlier, on the role of mathematics in the (sub-baccalaureate) technical work force.

Professor Steen is a prolific and talented writer of mathematics exposition and I urge you to read his Commentary, K-8 on the ADP Expectations page. This document can be downloaded from the link on the right side of this page.

I am in the process of composing a set of questions for Professor Steen. Both the questions and his replies will be printed verbatim in an upcoming post. Those who know my style should expect that my questions will be candid, direct but highly professional in nature and will reflect the concerns of my readership. Originally, my primary focus was to be on the Algebra II End of Course Assessment to be administered in the spring of 2008 to students in nine states in the consortium previously mentioned on this blog. However, I've indicated to Professor Steen that I would also appreciate his views on the current state of school mathematics in the US and his thoughts about the future direction of mathematics curriculum, instruction and assessment.

Algebra 2 End of Course Exam - Latest Info

Math teachers, math supervisors/curriculum leaders/specialists as well as students and parents should be interested in reading the latest information regarding this assessment that can be downloaded from the achieve.org website. School leaders should have already received this during the summer when it became available. The links are given below. Several months ago I posted information on this historic consortium that was formed via the American Diploma Project and Achieve. Nine states signed up to participate in this project, including my home state of NJ. Several districts in my state signed up to be part of the pilot project and students in these districts will be taking the assessment in the spring of 2008. There will also be a Field Test this October. As anticipated, a detailed enumeration of the core content for this assessment is now available and can serve as the basis of a syllabus for Algebra 2. From a cursory reading of the core content and the test specifications, I am impressed by the thoroughness of the development team. Moreover, I am struck by the balance struck between a traditional and reformed view of math curriculum and instruction. For example, the test will be in 2 parts, one allowing a graphing calculator and one without. Further, the core content repeatedly refers to student proficiency with multiple representations of functions - graphs, tables, verbal and symbolic expressions - what I've been calling the Rule of Four. Function modeling and problem-solving are considered central themes in the curriculum and the assessment will reflect this.

The core exam will have 60 questions, 50 of which are one-point multiple choice questions, 7 short answer (2 pts. each) and 3 free-response questions (4 pts. each). The non-multiple choice questions therefore account for about one-third of the point value of the test, a significant portion. In addition, schools, districts or states can select optional modules which will expand the assessment. These include Data and Statistics, Probability, Logarithmic functions, Trigonometric Functions, Matrices, Conic Sections and Sequences & Series. Since most algebra 2 curricula include several of these additional topics, I would expect some states to eventually select some of these.

There is no doubt in my mind that this is a positive step for raising the level of mathematics curriculum and instruction in these states and, hopefully, across the country if other states sign on (which I'm sure they will). The test will be developed by Pearson. I will be very interested in reading sample assessment questions when they become available. They will have a definite impact on change in curriculum and instruction. Teachers in courses leading up to Algebra 2 as well as the courses depending on Algebra 2 skills and concepts should also be vitally interested in this project. Algebra 2 is viewed as the gateway course to higher mathematics. The purposes of this project and the assessment are clearly stated in the document you can download (see link below).

Important Links:
Algebra 2 Exam Content and Overview from Achieve
Note: Click on the links under Related Content on the right side. The second link will download the complete pdf document enumerating the standards and detailed test specs. Save this document and share it with your colleagues at upcoming department and school meetings!

ADP Algebra 2 Benchmarks (with examples)

Achieve and the American Diploma Project Home Page

Singapore Math - Part III - Info from the 'Source'

I deeply appreciate zac's update on Singapore Math he recently published over at squareCircleZ. There's an excellent link there to a site that debunks many of the myths regarding the program (actually a commercial site but very informative). I was aware of most of this from other sites, but some information was new to me. I strongly commend it to your attention. I also asked zac if I could reprint my comment and his excellent reply. Fascinating stuff here...

In the end, regardless of whether or not students in Singapore are primed for these assessments (as in 'teaching to the test'), the bottom line is that the level of problem-solving that is assessed is higher than their grade-level counterparts here in the US. I never apologized for teaching to the AP Calculus Exam for the past 33 years. It has always been a high-quality challenging exam and became less predictable over the past 15 years with the Reform Calculus movement. Teaching to the test simply meant that I covered the syllabus and used released AP questions in addition to other resources to challenge my students. Shame on me! Of course I always added my own touches to the course like we all do.

Now for my comments and zac's reply:

1. zac–
   Thank you for debunking some myths (excellent site) and providing first-hand information. It doesn’t surprise me that there are many inaccuracies in reports I’ve heard about and read. It’s interesting to see that there isn’t a ‘one size fits all’ approach to the materials, however, the comments about ‘essence’ were the most telling. The ‘form’ of individual materials may change but the essential philosophy, not so much…

   It also seems that the supplementary workbooks in the program are significant and, at some point, I will need to order some of these materials to become more knowledgeable about the program.

   I have had the pleasure of teaching and providing SAT instruction for Asian students for the past 30 years (simply the demographic in my area), so I have come to know a great deal about their culture, after-school tuition programs, and their math curriculum. They found my comments about the superior performance of Singapore students interesting. Some characteristics they used to describe the tiny nation included ‘very clean, ‘very strict discipline in the schools’ and affluent. One student commented, “You don’t really believe that every student there can do all of these problems, do you!”

   My blog, however, focused on an actual ratio problem from the 6B Placement test which was really a 7th ‘grade’ pre-test from what I gathered. There was rich discussion about the heuristic of using fraction bars to represent units but, in the end, the quality and difficulty of the problem came through over all of the other conceptions and misconceptions about the program. That’s why the focus of my blog is problem-solving rather than debating overall philosophies which I generally consider futile.

   The calculator vs. non-calculator issue was mentioned in my posts and comments but it was not my focus. It’s not a secret that students with a solid foundation in arithmetic can regain computational proficiency if forced to. They didn’t enjoy it, and for the geometry questions, it was the most time-consuming part of the problem, but they did it - end of story there.

   Again, zac — the proof is in the materials and the level of complexity of the problem-solving. Many teacher and students were taken aback by how complicated some of these questions were. I commented that, if Singapore students, were exposed to these kinds of questions frequently over time, they wouldn’t find them so unusual or formidable. That made sense to them (of course I was only speculating that this was the case since I didn’t have many samples of problem sets).

   Your final comment about the irony of two nations whose assessment philosophies are somehow morphing into the other’s is fascinating but not a shock to me. I’ve read for many years that Asian nations have been watching American education closely and have been interested in fostering more creativity in their students and less rigidity. The problem-solving curriculum adopted by Singapore math in the 90’s is a reflection of some of this. But there’s a key point here that is often missed. We’ve had a problem-solving curriculum in this country for many years now, BUT THE PROBLEMS ARE NOT AS CHALLENGING! Philosophies don’t equate to performance. It’s all about the QUALITY of the materials and instruction as well as the overarching philosophy (the ‘essence’) - always has been, always will be. it isn’t just that students get to advanced topics earlier in some other countries. I’m more interested in the kinds of questions they are expected to solve. Do you see this as significant or do you believe it is the overall educational philosophy in Singapore that distinguishes it?

   I plan on posting another article on Singapore Math, referring to your latest post and including some of your links. i might even repeat some of your comments and mine if that’s ok with you. Of course, I will give you the attribution and link readers directly to this article. Thanks again…

   I am indebted to you for providing genuine and provocative information directly from the source. Thanks!

2. zac said,

   September 2, 2007 at 1:38 pm

   It isn’t just that students get to advanced topics earlier in some other countries. I’m more interested in the kinds of questions they are expected to solve. Do you see this as significant or do you believe it is the overall educational philosophy in Singapore that distinguishes it?

   The “educational philosophy in Singapore” (at the primary and secondary level) is very much focused on external standardized tests.

   I was very surprised when I got here to learn that the ‘O-Levels’ (end of grade 10) and ‘A-Levels’ (end of Junior College, ie 2 years of pre-university after O-levels) are administered from Britain! (The examiners are the University of Cambridge Local Examinations Syndicate.)

   At primary level (grades 1 to 6), the students have the joy of the PSLE (a Singapore-based series of 2-hour examinations in English, mother tongue, mathematics and science). [See also Bilingualism in Politics.]

   So to answer your question - if those questions are going to ‘come out’ in the examination, they will be drilled like mad in class. [One thing that never ceases to amaze me is the inherent ability of Singaporeans for rote learning. Read out a list of 20 words and they can happily recite them back to you. This is after years of testing in the Singapore system…] So I guess the ‘quality’ of the questions is a result of the examination writers’ enthusiasm for such questions.

   You may also be interested to poke around the Singapore Ministry of Education site.

   I might even repeat some of your comments and mine if that’s ok with you.

   Fine with me