[Update: Partial solution now in the comments. Fascinating discussion taking place about this innocent-looking problem...]
Figure 1
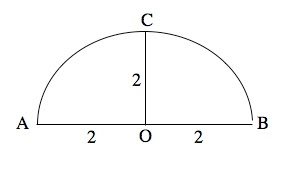
A standardized test sample problem I saw this evening, got me to thinking, which is often very dangerous. I will pose this 'open-ended' problem in terms of Jake making an assertion and Jack trying to convince him he's wrong. Jake keeps arguing and so does Jack. Who will win the argument logically?
Jake shows Jack a piece of wood he cut out in the machine shop in the shape of a circular arc bounded by a chord (See Figure 1 above). Jake claimed that the arc was not a semicircle, and, in fact, he claimed it was shorter than a semicircle, i.e., segment AB was not a diameter and arc ACB was less than 180 degrees. Jack knew this was impossible and argued: "Don't you see, Jake, that O must be the center of the circle and that OA, OB and OC are radii!" Jake wasn't buying this since he measured everything precisely. He argued that just because they could be radii didn't prove they had to be!
Here's your challenge for today:
(a) Find at least THREE different ways to PROVE that Jake is wrong, i.e., AB, in Figure 1, must be a diameter and O is the center. [Note: Can one assume perpendicularity?]
Figure 2
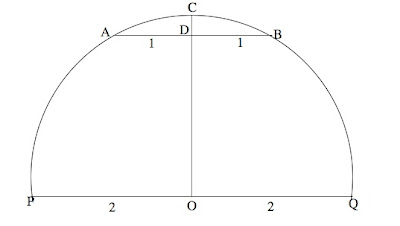
(b) Assume, in Figure 2 above, that PQ is a diameter, O is the center, chord AB is parallel to PQ and radius OC ⊥ AB. Determine the length of segment CD, and in particular, show that CD < DB.
(c) Refer to Figure 2, but let's generalize by removing the numerical values. Prove, in general, that for any chord AB parallel to and above diameter PQ, CD < DB.
[Pls note: We are no longer requiring that the length of chord AB be half of the diameter!]







12 comments:
right... my post without errors ^^,
c) easy ;) But I don't think these are the best proofs!
(let radius = r)
OC = OD + CD = r
[by pythag.]
DB = r/2, OB = 2
i.e. OD^2 = 3r/4,
hence OD > r/2
[or alternatively]
We know that OD = r/2 plus a little bit more, as angle DBO > angle DOB, hence i.e. OD > BC, i.e. OD > r/2
And OC = OD + CD
OD > 2/r
Hence CD < r/2
Hence CD < DB
Thomas--
Thanks for the nice reasoning...
I may not have made (c) clear. In this part, we are no longer assuming that DB = r/2. That's only for (b). In (c), we're asked to prove that CD < DB for ANY chord parallel to the diameter.
Also, did you mean that OD^2 = 3r/4 or (3/4)r^2??
Hi Dave,
When I first saw the figure, I thought you were going to discuss the "proof" that pi=2.
Next, I wondered why the figure had to be a semicircle: it could be a parabola. However, circular arc was a given and not to be questioned assumption.
For (c), I wonder if I can use the fact that the angle is >45 and thus the tangent is >1
For (a), one method is to use the angle in a semi-circle theme (a recurring theme, to which I guess I have had some contributions on this board :-))
Nice problem, though. I need to find the time to think more about this.
TC
This was fun!
(a)
1. Draw AC and BC. Since triangles AOC and BOC are isosceles, and since AB is given as a segment, it is easy to show that angle ACB is half of 180 degrees. Then as TC says, AB must be a diameter.
2. If O is not the center of this circle, it is the center of some other circle containing A, B, and C. But then these 2 circles would intersect in 3 points. This is not possible, unless the circles are the same.
3. Similarly to #2, but then triangle ABC would have 2 different circumcircles, which is not possible.
4. If you were also given that OC is perpendicular to AB, you could use the reasoning given in (c) below.
5. Put O at the origin, and define the hypothetical center of the circle as P(x,y). Use the distance formula to calculate x and y, given that the radii AP=BP=CP.
(b) Skipped this one and went straight to (c). I couldn't see that the numbers made any difference.
(c) Draw OB. Angles OBC and OCB are equal.
Angle OBC = angle OBD + angle DBC, thus angle CBD < angle OCB.
tc--
i forgot about the pi=2 proof - remind us!
For part (a),I SEEM to have omitted the condition that OC is perpendicular to AB. If OC were NOT perp to AB, would it still follow that it's a semcircle? (see my 2nd and 3rd methods below).
Certainly the theorem regarding inscribed angles and intercepted arcs (special case: right angles and semicircles) would do it, provided we had the perpendicularity condition. One of my SAT students came up with that one fairly quickly.
METHOD TWO: None of them considered the defining property of a circle: Point O is equidistant from points A, B and C. Therefore O is the center of the circle containing those points and there can only be one such circle since 3 non-collinear pts determine a unique circle. Of course 3 such points also determine many other geometric objects such as a parabola, a triangle, a plane, etc...
A third method involves angles and sides but without trig. Nothing wrong with trig or coordinate geometry, but I wrote this investigation to help students develop insight into angle-side relationships, inequalities and the indirect method of proof.
METHOD THREE (I'll get you started and then some). I am NOT assuming that OC is perp to AB here. Draw chord AC. From the equal sides of triangle OAC, it follows that angle OAC = angle OCA. Reasoning indirectly, assume that O is NOT the center of the circle! Let point P (not shown) represent the center and from the initial assumptions, P would be below segment AB. The radii PA and PC are equal. Now consider isosceles triangle PAC and show there is a contradiction!!
What's nice here is that we are not requiring that OC be perp to AB!! Personally, the generality of this proof and the indirect method of proof appeals to me. Students do not see enough of these kinds of arguments. Do you think someone came up with this line of reasoning in my SAT class?
Note that in the other parts of the problem we are given the perpendicularity condition because the purpose has changed.
I think there's a whole lot more to be said here, but I'm getting tired! Remember the title of this post - A 'SIMPLE' GEOMETRY PROOF?? Is there more here than meets the eye? Have fun and keep commenting...
If we can assume that OC is perpendicular to AB, then here are two more approaches:
Extend OC to P, the hypothetical center of the circle.
CP = OC + OP
Draw radius BP=CP.
BP = OC + OP
But OC = OB, so
BP = OB + OP.
The hypotenuse is equal to the sum of the legs? Only if OP = zero!
Or, using the same drawing, by the Pythagorean Theorem:
BP^2 = OB^2 + OP^2
BP = CP = OC + OP = OB + OP
(OB + OP)^2 = OB^2 + OP^2
[Again, this is true only if OP = zero.]
denise--
nice!!
i like both proofs equally well and more than mine...
Denise, the issue for me is: Do most students in ms or hs have the opportunity to develop their reasoning like this? How many out there might feel that this kind of 'proof' is suitable only for the honors crowd? My personal feeling is that many more students can learn how to think like this if given more opportunities and models to follow. After seeing your paragraph proof, would some students be able to tackle a similar problem? Don't know if we don't try! Did you find this problem trivial or engaging? Is looking for more than one solution overkill or worthwhile? My experience working with many gifted students over the years is that often these students 'see' a solution fairly quickly and then turn off. Requiring each group of students to devise 2 or more proofs can be very beneficial in my opinion.
Now, what do you think about the non-perpendicular case?
Thomas came up with some good ideas for (c). I'm waiting to hear from others on this one...
sorry, denise!
i missed you first comment.
again, very nice job on (c). That's the method I used.
Again, I would ask: Is there a place for these kinds of 'challenges' in our current geometry curriculum? If yes, then we need resources containing many such 'challenges.' After a while, students would become accustomed to higher level thinking and more would feel successful.
Now for the issue of proof! Your comfort level in writing these paragraph proofs demonstrates two things to me:
(A) You're good at them.
(B) You enjoy them!
Now, how do we begin to get our students to this place!?!
We could devote 20-30 posts on the issue of proof but enough for now!
Thanks for your contributions.
Dave
It would be wonderful to have a resource of this type of problem, especially if it was arranged by ability levels---say, from upper elementary or pre-algebra on through high school. Do you know of any?
Hi Dave,
The pi=2 proof goes as follows. If you have a semicircle with a diameter 2 and center at (0,0). The length of the arc is pi.
Now draw two semicircles of diameter 1 with centers at (-1/2,0) and (1/2,0) but one going above the line and one below the line. The total length of the arc is still pi.
You can continue this process again and again (4, 8, 16 .. semicircles), and at each point the length of the arc is pi. In the limit, the arc approaches the diameter (which is of length 2). Thus pi=2
TC
Along the lines of my last comment, looking for a resource of such problems... Does Blogger let you organize your archive by categories rather than by dates? That would be ever-so-much more helpful in finding a problem that fits my next lesson.
Post a Comment