Unit Fractions - Pyramid Power?

Update as of 6-2-07: All solutions to the problem below are now posted in the Comments section. Also, read Eric Jablow's astute comments and his challenge to students!

The following problem is well-known, however it is an excellent exercise for middle schoolers and as a challenge for older students as well.
Target Audience: Grades: 6-12
Prerequisite skills: Basic understanding of fractions and simple operations
Develops: Logical thinking, Systematic Counting/Listing, Fraction Concepts, Structure of Mathematical Proof
Recommended Classroom Organization for this activity: Students working in groups up to 4.
Online Resource: Here's one of the best sites on Egyptian Fractions I have found on the web. The problem is discussed but not solved!

Introduction for student:
A unit fraction is defined as 1/n, where n is a positive integer greater than 1.
The number 1 can be written as a sum of 3 unit fractions in 3 ways:
1 = 1/2 + 1/3 + 1/6
1 = 1/2 + 1/4 + 1/4
1 = 1/3 + 1/3 + 1/3
No other ways (other than rearrangement) can be found using the following reasoning:
The largest of the 3 fractions could not be less than 1/3. Why?
If 1/3 is the largest fraction, then the larger of the remaining fractions could not be less than 1/3. Why?

Here's your challenge:

There are 14 ways to write 1 as a sum of four unit fractions of the form:
1 = 1/a + 1/b + 1/c + 1/d, where a ≤ b ≤ c ≤ d.
Make a list of all of these ways. Have fun! Uh, no calculators please!

Investigating an SAT Algebra Problem - Going Beyond the SAT Strategy for Deeper Meaning

[Update as of 6-2-07: Solutions to most parts of the problem are now posted in the Comments.]

The following problem is typical of a somewhat difficult Algebra 2/Precalculus type of SAT problem. Students who have been shown the 'quick and easy way' to solve this definitely have an advantage when taking the test. This has been developed into an activity for Algebra 2 students who might be taking the SAT on June 2nd. However, the activity explores more than just a strategy for solving the problem efficiently to get an answer for the test. Students will be asked to solve the problem the traditional way as well and analyze why this question should not appear on the test. Two separate graphical interpretations are included to deepen student understanding, one for Algebra 2 students and a more sophisticated one for the Precalculus class. Is it worth spending 25 minutes or more on one problem in class? I'll let you judge...

Consider the system of equations:
1/x + 1/y = 1/4
1/(x+y) = 1/3

(a) (SAT-type of thinking): Show that xy = 12 (without solving for x and y).
Note: I'm giving the 'answer' here so that students will focus on the method; also for part (f).

(b) (Algebra 2): Solve the system (i.e., find all possible solutions for x and y). Write your answer(s) as ordered pairs.

(c) Verify, algebraically, that your solutions satisfy the original equations.

(d) Explain why this exact question should not appear on the SATs (although this type of question has appeared frequently).

(e) (Precalculus extension): Graph the system:
1/x + 1/y = 1/4
1/(x+y) = 1/3
Notes/Hints:
You must graph each equation separately. Do not replace the first equation by xy = 12.
Hint: Solve each equation for y.

(i) Explain clearly why the graph of the first equation has both vertical and horizontal asymptotes. Label these in your graph.
Note: The customary way is to solve for y first. See if you can also determine the asymptotes without changing the form of the equation!

(ii) Does your graph of the first equation contain the origin? Explain why or why not.

(iii) How many solutions of the system are evident from the graph? Explain the reason for this.

(f) (Algebra 2): Now solve the system
x+y = 3
xy = 12

(i) In what way is this system equivalent to the original system?
(ii) How many solutions of this system are evident from the graph? Explain the reason for this.

'Carnival' of MathNotations 5-25-07

New feature...

I apologize for stealing the 'Carnival' term - I couldn't resist it. If the Carnival people want equal time, here's my plug for one of the best: Visit the home page of the Carnival of Mathematics - we are all indebted to Alon Levy (I hope I got that right!) for developing and maintaining this wonderful venue for the math-minded out there who may not have time to discover or visit all of the outstanding math blogs on the web. Considering that I'm hosting the Carnival the week of June 15th, I thought this attempt could also be a dry run...

It's easy to miss some interesting dialogue when we jump from site to site on the superhighway. I watch how my students and my children surf the net- if they don't see what they want on a page within 5-10 seconds, they're gone!

Since some of the most interesting 'stuff' often takes place off-post in the comments section, I thought it would make sense to summarize some of this at the end of the week. I'll probably tire of this after a couple of weeks, or choose to do this every other week like the real Carnival of Mathematics, but I'd like to try it anyway.

I apologize in advance to my other faithful readers and expert commentators for any errors of omission. Their contributions enrich this blog and their continual support inspire me to maintain these efforts. I will add more as I sift through my posts from the past two weeks. For now here are some highlights from the past 8 days.

• A series of posts (Part I and Part II) this past week have focused on developing meaning and application for exponential functions (and their relation to geometric sequences and series) designed for Advanced Algebra classes. These extensive classroom investigations use the concepts of mortgages, stressing the ideas behind those esoteric formulas. There are full-blown activities with open-ended questions and data analysis using the graphing calculator. Screen shots of data tables from the TI-84 enhance the activity. Further related activities to follow...
  
• A set of Thinking Outside The Box problems came up earlier that stimulated some great comments and ideas from Denise (author of the excellent site letsplaymath) and others. This has led to an ongoing discussion of the sticky problem regarding the smallest positive integer having a given number, N, of factors. The problem has been solved if N is prime, or if N is a semiprime (N = pq, where p,q are distinct primes), but it's not clear that we have a general solution. Someone out there must know the algorithm for finding this number - pls share it! I haven't yet posted answers or detailed solutions to some of the questions, so stay tuned.
  
• TC, another of my dedicated readers, posed the pi = 2 'proof' introduced first in the comments here and continued in the comments section of Part I of the mortgage problems. I challenged my Calculus class to explain the fallacy in this limit problem and one student, Matthew, came up with a pretty nice solution. This problem could easily be a post in and of itself with many possible extensions. TC presented an excellent 'curvature' argument and I added some thoughts of my own.
• Eric Jablow, our math/computer science expert, suggested 3 excellent algorithms (bisection method, method of false position and Newton's Method) for approximating roots of an equation. These are worth sharing with our algebra and precalculus students as well as those in Calculus and Computer Science. These comments are found under the post entitled Catching Up and Preview of Coming Attractions.
  

Pls give me your feedback. If you think the title is too presumptuous, say so! If you think it's a waste of time to summarize only a week or so of posts and comments, let me know that too. If you have something nice to say, I'll accept that as well! Signing off for now...

Puff the Magic Mortgage Part II

OVERVIEW OF PART II
We will continue our investigation of mortgages. In parts (a), (b) and (c) below, you will analyze the effect of accelerating repayment by paying off the loan in one year with 2 equal payments at 6-month intervals, instead of one payment each year for 2 years, [NOTE: Some lenders do not allow this without a prepayment penalty, but we'll assume Stan the Mortgage Man is sorry for the error of his ways and wouldn't charge this.]

In (d) we will analyze data tables corresponding to the same loan of $100 but there will now be several payments over the course of one year (you will need to determine how many).

(a) From your knowledge of compound interest you know that if payments are made semiannually (in 6 month intervals), the interest rate is divided by 2, the number of interest periods; thus the rate would be 5% on each of these payments. Using an analysis (algebraically) similar to part of the earlier activity, show that each of these equal payments would be $53.78.

(b) How much is saved in total by repaying the debt in one year by this method, compared to one payment a year for 2 years? Explain why this happens. [By the way, if your parents do make mortgage payments, ask them if they are making two payments a month and, if so, why?]

(c) What could you do to reduce the total payment even more, assuming that the debt is paid off in one year?

(d) Study the 4 tables below. The data in Y1, Y2, Y3, Y4 all relate to the loan of P = $100 at 10% annual rate of interest. The loan is repaid at the end of one year but is paid in several payments. We will not tell you what the meaning of each of the columns (functions) are. That's part of the challenge! Your job is to interpret the data and respond to the following questions:

(i) How many interest periods (payments) are there? How do you know? Be careful here!
(ii) Which column (function) corresponds to each monthly mortgage payment. Give reasons.
(iii) Which column corresponds to the amount of debt remaining after each payment? Give reasons.
(iv) Which column corresponds to the amount paid toward the principal (P = $100) at each payment? Give reasons.
(v) Which column corresponds to the amount of interest paid at each payment? Give reasons.
(v) The total dollar amount of which column should be exactly $100? Explain why.
(vi) How much is the first interest payment? How much is the first payment toward principal?
(vii) Explain the meaning of the zero value in Y4.
(viii) Which function (column) is best modeled by an exponential function of the form
f(x) = a ⋅ b^x-1? Determine the values of a and b and their relationship to the loan.

Hint: Consider a simpler example. Suppose the first few terms in a sequence or list are 3,6,12,24,... This is known as a geometric sequence because, starting with the 2nd term, the ratio of each term to the preceding term is constant: 6/3 = 12/6 = 24/12 = 2. The function that describes this sequence is 3 ⋅ 2^x-1, for x ≥ 1. Thus, every geometric sequence can be modeled by an exponential function. Use this approach to answer this part.

Taking the Magic out of Mortgages Part I: Exponential Functions and Geometric Sequences to the Rescue

[Note: For an exceptionally clear and definitive exposition of all things financial, the best resource I have found is MoneyChimp. There are interactive calculators to thoroughly understand the concepts in this post and much much more. More importantly, for math nerds like me, the formulas are explained and, in some cases, derived. The mathematics is accurate and the analysis is excellent. Enjoy it!]

In Algebra 2 and Precalculus (or whatever it may be entitled in your local schools), students often do compound interest problems. Typically, the author of the text and/or the instructor will derive the formula for what your original investment of P dollars will be worth in t years, if interest is compounded n times per year for t years at an annual rate given by r (a decimal for this discussion):
Compound Interest Formula: A(t) = P(1+r/n)^nt.

This is a nice practical application of exponential functions, exponential growth in particular. A similar, but more sophisticated, concept applies to annuities and amortization of a mortgage (paying off debt over time in n equal payments). In both an annuity and a mortgage, the original amount of money (whether it's the amount invested or the debt you owe) generally decreases over time. In an annuity, you receive a fixed amount at the end of each period, whereas, in a mortgage, you pay a fixed amount. In an annuity, your original investment is earning (accruing) interest (it may be possible to 'live off' the interest and not touch the principal), while you are receiving periodic equal payments that are deducted from your account. A central concept in both annuities and mortgages is that that interest is applied before receiving an annuity payment or before making a mortgage payment.

The following is the first part of an activity introducing students to the mysteries of mortgage calculations. The fact that the formulas for monthly payments or the decreasing amount of debt seem very intricate lead many to believe that this topic is too sophisticated for most secondary math students. Just give them the formulas, mention that it is related to exponential functions and let them plug it all into their graphing calculators. We know most adults, other than those in the business of lending, punch the numbers into the computer and read the results. Before calculators, bankers would look it up in those mortgage tables on some well-worn-out card. This activity may demystify a little bit of this. Students need good algebra skills, knowledge of exponential properties and functions in particular, a basic knowledge of compound interest and background in geometric sequences and series (later on). I am well-aware that sensitivity is needed here for students whose parents do not own a home, however, all students can benefit from these ideas since these principles apply to far more than a monthly mortgage payment.


STUDENT ACTIVITY
You can find many excellent web resources for mortgage calculations. You can also find the actual formulas for all of this either in your text or in other sources. Most of us would probably use the built-in applications typically found on a graphing calculator or more likely use those free mortgage calculators all over the web. In this activity you will take an active role in the process of borrowing and lending and see what lies behind those sophisticated formulas.

In actual practice, mortgages can range from less than a hundred thousand into the millions of dollars. Therefore, these loans are typically repaid over 5, 10, 15, 20, 25 or 30 years to make the monthly payments more manageable. In this activity you will be borrowing a small amount and considering an oversimplified form of repayment, leading up to more general considerations.

You will be borrowing $100 from a reputable lender, Stan, The Mortgage Man.
Stan is charging the going rate at the moment, which is 10% compounded annually.

(a) If you repay the loan in one year, explain why your single payment would be $110.
(b) If you agree to repay the loan at the end of two years, in one single payment, explain why that single payment would be $121?

Discussion: Parts (a) and (b) should remind you of the compound interest formula you've learned:
One year re-payment: 100(1+0.1)¹
Two year re-payment: 100(1+0.1)²

Surely, increasing the payment schedule to TWO payments over two years or one year, cannot be that much more difficult? Let's find out...

(c) This time you will make two equal payments over two years. Stan gives you the repayment schedule: Two equal payments of $60. He explains it as follows: The loan (your debt) of $100 is divided into two equal payments of $50 each. The interest charges are $10 (10% of the amount you borrowed) on each payment. Explain the mistake that Stan is making (or is he trying to take advantage of an unsuspecting borrower who didn't pay attention in algebra?). We're not asking you to correct Stan's error here - just explain why his calculation is either wrong or unfair.

(d) Now that you figured out that the two equal annual payments should not be $60, we will tell you what the actual payments would be according to mortgage formulas:
Each annual payment is $57.62 (rounded to the nearest penny).
Show why these two payments correctly repay the loan of $100 and the interest that is due on each payment. Show method clearly. Use calculator as needed.

(e) Do you think you could figure out an algebraic way to determine those equal payments of $57.62? You are about to...
Let A represent the equal annual payments you will make.
At the end of the first year, before you make your payment, you owe $100(1.1) = $110.00. Now the fun begins:
(i) Represent, in terms of A, the amount of debt (loan + interest) you will owe AFTER you make your first payment.
(ii) Represent, in terms of A, the interest you will be charged by the end of year 2 BEFORE you make your final payment.
(iii) Represent, in terms of A, your debt, AFTER making your final payment.
(iv) What should be the numerical value of your debt AFTER making your final payment? Now, write an equation and solve for A. You should come up with $57.62!

(f) Are you up to the challenge of solving for the general formula for A given an original loan of $P at an annual interest rate of i (expressed as a decimal)? Of course, you are! For now, you only need to do this for TWO payments, just as we did in (e). Of course, your formula for A should be in terms of P and i.

More to follow...

Helping Students Think 'Outside the Box'...

[Update: I'm adding an additional problem at the end. This question seems to be of interest to some since I've seen it in a Google search for awhile now. Answers and solutions to some of the problems will shortly appear in the comments.]


The issue for me as a math educator has always been:
How do we enable children to think conceptually?

Here are some standardized types of questions each of which can be solved by a variety of methods.

In each of the problems below, there is a conceptual approach that requires skill, knowledge and some insight. We all know as educators we can do something about the first two (provided students are given enough practice and they do it!), but how do we develop insight? I can only tell you how my insight improves: When I tackle harder problems or those requiring me to 'think differently'. I am sure there are those out there who are able to invent these methods on their own, but, as for me, I have to work at it and think about it!

The first 3 questions involve ratios. Since we know how the current generation feels about fractions, these may cause students to feel some frustration!

See if you can find an 'insightful' or conceptual approach. Also, ask yourself how most middle or secondary students would approach these:

1. Background Terminology: For those of the younger generation who may not have heard of the term proper fraction, it means a ratio of positive integers in which the denominator is larger than the numerator. Thus, 4/3 and 3/3 are improper; 2/3 and 1/3 are proper. Also, the phrase 'in lowest terms' means that the greatest common factor of the numerator and denominator is 1. (But everyone knew that, of course!)

If 10/n, 14/n and 15/n are proper fractions in lowest terms, what is the least possible positive integer value of n which is not prime?

2. For how many integer values of n is 11/n between 1/9 and 1/10?
Note: Is this an algebra problem? A guess-test 'plug-in' problem? A calculator problem? Or just a fraction 'exercise'?

3. Fahrenheit temperature is related to Celsius by the equation: F = (9/5)C + 32.
An increase of 36 degree F. is equivalent to an increase of how many degrees Celsius?
Note: Many students struggle with an approach here. Some try it algebraically, most plug in some initial temperature, virtually none I have observed think conceptually about the meaning of ratios.

4. A cube 6 inches on each edge is sliced 'horizontally' to form 2 congruent rectangular solids. If these 2 solids are joined to form a rectangular solid which is not a cube, the surface area of this resulting solid is how many more square inches than the surface area of the original cube?
Note: Some youngsters simply 'see' this with little or no calculation! I guess you could say, they really 'think outside the box!' (sorry 'bout that...)

5. What is the smallest positive integer having exactly seven factors?

Catching Up and Preview of Coming Attractions

Gee, so why don't I have answers to the parabola-circle problem posted yet? It's coming later tonight or tomorrow -- hang in there...

Also, I'm working on a major exploration of exponential functions and geometric series via an analysis of Mortgage Calculations. I set a very high standard for myself so it's still under construction. I think it will be worth waiting for since it involves derivation of formulas, analysis in special cases, and graphing calculator investigation (not merely relying on a built-in application), etc...

When Curves Collide: Quadratic Systems Explored...

[Another Update: Mutiple solutions to (a) and (b) are now provided in the comments (as of 10:50 PM 5-17-07).]

Target Audience: Algebra 2, Advanced Algebra, and beyond...

The previous post challenged students to consider 'basic' properties of circles and triangles. Now we will look at systems of quadratics - circles and parabolas in particular. The purpose here is to help students go beyond the standard algorithms of solving systems, by analyzing a general type of system using a parameter r. The use of parameters has become the norm on the AP Calculus Exam. Algebra students may benefit from an early introduction.


OVERVIEW FOR INSTRUCTOR
Consider the system:
x² + y² = r²
y = r² - x²

Here, r denotes a positive constant. Depending on the value of r, this system will have either 2, 3, or 4 solutions!

Simple problem of a parabola intersecting a circle, right? We will assume here that students have already solved specific cases of such systems both graphically and algebraically (substitution, etc.). They have been shown that parabolas and circles may intersect in 0, 1, 2, 3, or 4 points. As a review, begin this investigation by asking pairs of students to sketch (no equations here) graphs depicting each of these cases. That visualization is a powerful context for the algebraic solutions and may motivate the students to consider why varying the parameter r in this lesson leads to different conclusions. This type of analysis goes beyond standard problems and prepares students for the open-ended free-response types of standardized or AP questions they will later encounter in high school or college.

FOR THE STUDENT:

(a) r=1
Solve the following system first graphically, then algebraically:
x² + y² = 1
y = 1 - x²
This system demonstrates that a quadratic-quadratic system may have ________ (number) solutions.
For this system, the points of intersection are ___________________________.
For x between -1 and 1, the parabola is (above, below) the circle.

(b) r=2
Solve the following system first graphically, then algebraically:

x² + y² = 4
y = 4 - x²

This system demonstrates that a quadratic-quadratic system may have ________ (number) solutions.
For this system, the points of intersection are ___________________________
Restrict the domain to -2 ≤ x ≤ 2. For what values of x is the parabola above the circle in this system? Below the circle?

(c) What set of positive values of r have we not yet considered?
For such values of r, make a conjecture about the number of points of intersection of the system:
x² + y² = r²
y = r² - x²

Now choose a particular value of r in this set, say r = 1/2. Check the validity of your conjecture by solving the system for this particular value both graphically and analytically (algebraically).

(d) Analyze, algebraically, the following system for all positive values of r. Show carefully that your algebraic solution leads to 3 distinct cases for r:
x² + y² = r²
y = r² - x²
For each case, give the solutions (ordered pairs) in terms of the parameter r.
Explain why, for all positive values of r, there will always be at least TWO solutions of this system. That is, the possibility of zero or one solution does not exist for this system...

A Simple Geometry Proof or Circular Reasoning??

[Update: Partial solution now in the comments. Fascinating discussion taking place about this innocent-looking problem...]

Figure 1

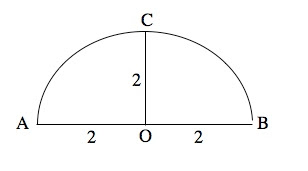
A standardized test sample problem I saw this evening, got me to thinking, which is often very dangerous. I will pose this 'open-ended' problem in terms of Jake making an assertion and Jack trying to convince him he's wrong. Jake keeps arguing and so does Jack. Who will win the argument logically?

Jake shows Jack a piece of wood he cut out in the machine shop in the shape of a circular arc bounded by a chord (See Figure 1 above). Jake claimed that the arc was not a semicircle, and, in fact, he claimed it was shorter than a semicircle, i.e., segment AB was not a diameter and arc ACB was less than 180 degrees. Jack knew this was impossible and argued: "Don't you see, Jake, that O must be the center of the circle and that OA, OB and OC are radii!" Jake wasn't buying this since he measured everything precisely. He argued that just because they could be radii didn't prove they had to be!

Here's your challenge for today:

(a) Find at least THREE different ways to PROVE that Jake is wrong, i.e., AB, in Figure 1, must be a diameter and O is the center. [Note: Can one assume perpendicularity?]

Figure 2

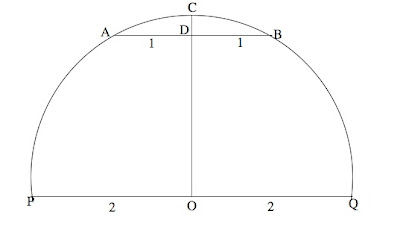
(b) Assume, in Figure 2 above, that PQ is a diameter, O is the center, chord AB is parallel to PQ and radius OC ⊥ AB. Determine the length of segment CD, and in particular, show that CD < DB.

(c) Refer to Figure 2, but let's generalize by removing the numerical values. Prove, in general, that for any chord AB parallel to and above diameter PQ, CD < DB.
[Pls note: We are no longer requiring that the length of chord AB be half of the diameter!]

Substitutions in Calculus - U Can Do It (Maybe Not)

With the AP Exams this week and the year coming to an end, the timing of this post is way off but I wanted to share some thoughts about using u-substitution in integration (and differentiation). Every text promotes it, I've been teaching it for years, but, like so much else in mathematics, u-substitution is really a form of 'information-hiding' that may sacrifice understanding for the sake of brevity. While I believe using u in place of f(x) is an important technique for some calculus algorithms, experience has shown me that keeping f(x) in the formulas works better during the learning phase. In this post I will show how using f(x) in the formulas for integrals may help students deal with the variety of functions they encounter when integrating using the 'Inverse Chain Rule' (I coined that phrase to help students recognize that the f'(x) factor disappears when anti-differentiating (integrating) and appears when differentiating. If your first reaction is that these formulas are more complicated, I think you might need to actually experience the difference in students' reactions. There's no substitute for that!!

If you've already tried both approaches, let me know which form worked better for a majority of your students. My impression is that many students are at first overwhelmed by the varieties of different forms that appear in the typical set of exercises following this lesson. We can say that they're basically all the same, but it doesn't appear that way to the novice!

Outline of Lesson:
The topic was introduced by reviewing several differentiation problems using the General Power Rule for d/dx(f(x)), using the Chain Rule. Each derivative was immediately followed up with the corresponding antiderivative problem. The idea that both (f(x))ⁿ and f'(x) must be present in the integrand was emphatically stressed. I repeatedly asked the question, "What is the f(x) here?" then, "What would f'(x) be?" Also, "Is the exact f'(x) in the integrand?" If not, we discussed the method of supplying a missing numerical factor and its reciprocal, using properties of antiderivatives, etc. They seemed to get this, struggling a bit with the idea of using differentiation in an integration problem, a natural source of confusion at first. We made sense of all this for the first few examples by differentiating our answer to check it. As with all new ideas, some caught on quickly, others had not yet internalized it after 3-4 examples because I too quickly moved into variations on the basic form before they had really processed it.

The following are the 'forms' that helped them adjust to the variety of trigonometric and other types of examples. This seemed to eliminate much confusion...

Some ∫ form(ula)s:

1. (General Power Rule): ∫f'(x)(f(x))ⁿdx = (f(x))ⁿ⁺¹ /(n+1) + C,
n ≠ -1

2. ∫cos(x)sinⁿ(x)dx = (sinⁿ⁺¹(x))/(n+1) + C, n≠ -1

3. ∫f'(x)sin(f(x))dx = -cos(f(x)) + C
OR
4. ∫f'(x)cos(f(x))dx = sin(f(x)) + C
Note: There is a critical but subtle difference between #2 and #3, even though they are both applications of the Chain Rule.

5. ∫f'(x)sec²(f(x))dx = tan(f(x)) + C
6. ∫f'(x)sec(f(x))tan(f(x))dx = sec(f(x)) + C

7. ∫f'(x)e^f(x)dx = e^f(x) + C

8. ∫f'(x)/f(x)dx = ln|f(x)| + C vs. ∫du/u = ln|u| + C

There are many others, but you get the idea.
If you still believe that the u-forms are so much simpler, that's fine, since I like the u-method as well and it is needed later on. I think all experienced math teachers latch on to their favorite methods or models because they have worked effectively with many students. However, I do not believe that any method will be effective for all due to learning style issues. There may be some students who will simply feel more comfortable and perform better if they use Method A vs. Method B.

I should have included some of the actual examples used, but...

What goes up...Applying Quadratic Functions

This question was inspired by a released SAT question from a couple of years ago. Some of you may recall this question that appeared on the first released Sample Test for the 'new' SAT. Can you think of some reasons why this question was used by ETS as a Sample problem?

Because the height function given was not exactly in 'standard' form (using a,h, and k), even the strongest students I administered this problem to resorted to complicated algebra or used a physics formula (s = 0.5at²+...). They missed the point that when given the vertex of a parabola you're given more than just an ordered pair! I believe our students need more experience with this type of 'free-response' application. We see these in some textbooks but is enough time devoted to them or is that left to the physics teacher?

As usual, I've modified the question and developed it into an open-ended problem with several parts. Pls don't get exercised about the lack of reality of the physical model!

A model rocket is projected vertically upward from a point 877.5 ft above the ground and after 2.5 seconds reaches its maximum height of 1440 ft. We are given its height above the ground as a function of t:

h(t) = p(q-3t)² + r, where t is in sec, h is in ft; p, q, r are constants.


(a) Determine the values of p, q and r.

(b) Rewrite the given function in 'standard' form: h(t) = a(t-h)² + k.

(c) Determine, algebraically, all values of t for which h(t) = 1080. Explain, in terms of the motion of the rocket, why there are exactly 2 such values.

(d) After how many seconds did the object hit the ground? Use algebra.

(e) Verify your results by analyzing the function using graphing calculator technology.

Going off on Tangents without Calculus!

[Update: Answers to several of these are now posted in the comments. Also, some nice discussion as well.]

To challenge Geometry, Algebra 2 and Precalculus students, we can always go back to our old friend, coordinate geometry. When I learned this way back when, it was referred to as 'Analytic Geometry'!

The following is a series of problems that review some basics of circle geometry, coordinate methods and lots of good algebra. Most of these can be found elsewhere and there are several different methods of approach. The method I'm suggesting for the first few problems is a bit different, i.e., determining the general equation of a tangent line to a circle, whose center is at the origin, at an arbitrary point on the circle. It used to be a standard formula taught in that above-mentioned course, but few students see it nowadays. Try it as in-depth investigation or exploration, starting in class or as an extension (long-term assignment or extra credit). Our AP calculus students can benefit from 'open-ended' experiences like this before they get to the AP course.

STUDENT ACTIVITY

For the first 2 questions, consider the circle whose center is at (0,0) and whose radius is 5.

1. Determine the equations of the tangent lines to this circle at the points (3,4) and (4,3). Write the equations in the form Ax+By = C. What do you notice about the results?
2. Based on the pattern of your answers in question 1, make a conjecture about the equation of the tangent line to this circle at an arbitrary point (x₁,y₁) on the circle. Now verify your conjecture 'analytically', i.e, using coordinate methods and algebra.

3. Based on the above patterns, make a conjecture about the equation of the tangent line to the circle of radius r, center (0,0) at an arbitrary point (x₁,y₁) on the circle. Verify your conjecture.

4. Now we return to the original circle of radius 5, center (0,0). Write the equations of the two tangent lines to this circle, which have a slope equal to -2. Again, write them in the form
Ax+By=C.
Note: There are many many approaches here. Discuss at least two!

5. Now, let's go outside the circle. Consider the circle of radius 1, center at (0,0) and let P have coordinates (0,2). Determine the equations of the two tangent lines to the circle through P. Also indicate the coordinates of the points of tangency.
[This 'special' case can be handled with very little algebra or computation.]

6. To generalize a bit more, consider the circle of radius r, center at (0,0) and let P have coordinates (0,2r). Again, determine the equations of the two tangent lines to the circle through P. Also, express the coordinates of the points of tangency in terms of r.

7. Final Generalization: Consider the circle of radius r, center at (0,0) and let P have coordinates (0,b) where b > r. Again, consider the 2 tangent lines to the circle, which contain P. Write an algebraic expression for the coordinates of the 2 points of tangency in terms of r and b.